Forms of Flexibility

6 × 6 × 6 × 2


I first wrote this note for the press release when I showed 6 × 6 × 6 × 2 at Bortolami in 2018. I revised it in 2020 and added some further remarks.

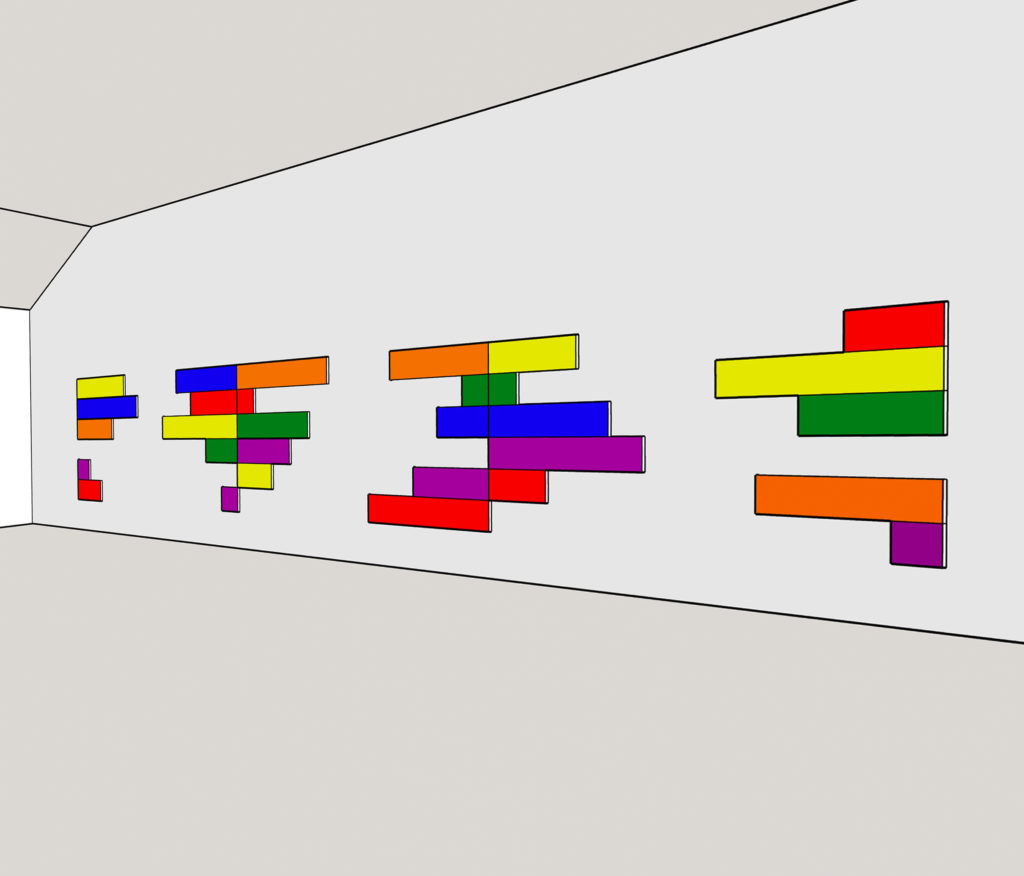
6 × 6 × 6 × 2 is a painting in multiple parts on two facing walls. The origin of the work was my visualizing two shapes the same height that were separated by a space. The edges of the shapes that faced each other were jagged, like saw teeth or as if notched, but the notches were different depths. The shapes were close enough to each other that their irregular edges made us see the space between them. (When the edges of adjacent paintings are straight and parallel, as most are, we don’t notice the space between them unless it’s unusually narrow or unusually wide.) The shapes’ irregular edges implicate the space between them, making it a part of the shapes even if it lies outside their material limits. In relation to the shapes, the space between them is a negative space. This term ordinarily refers to the part of a representational painting that is not its subject, what we can loosely call the painting’s background. In the ordinary use of the term, negative space is within the material extent of a painting. By calling the space outside the material limits of the shapes a negative space, I am claiming that it is as much a part of the shapes, as if as much within them, as a negative space is within the material extent of a representational painting.

This simple relation between two shapes and the space they produce between them quickly turned into a painting in multiple parts on two walls that face each other. Additional parts produce additional irregular edges and hence additional negative spaces.

The relation between the subject of a representational painting and the painting’s negative space is that of complements. Together they occupy the material extent of the painting. In 6 × 6 × 6 × 2 the relation between the irregular edges of the shapes and the negative spaces they produce beyond their confines is also that of complements. The work extends my interest in working with complementary relations but in a new register, that of shape.

6 × 6 × 6 × 2 is organized in parts I call stacks. Each stack consists of six horizontal panels each one foot high, each ranging in width from one foot to six feet in increments of one foot. Each of the six widths occurs once in a stack. Each panel in a stack is one of the six colors in the color circle, the same set of colors I have used in earlier work. Like the six widths, each of the six color occurs once in a stack.

A ready means for producing a chance result, which by definition is noncompositional, is a die: six faces, each with a different number, one through six.

I rolled a die to determine the width of the bottommost panel of the stack at the left-hand end of the left-hand wall. The die came up five, so the panel was five feet wide. After the die told me the width of the panel, I rolled it again to determine its color. One was red, two was orange, and so on. I rolled a six, so the color of the panel was violet. And so, working upward, I proceeded panel by panel to make the first stack. If the die gave a width that was already in the stack, I rolled it again until it gave a width not already in the stack, and the same went for the color. The same procedure made the rest of the stacks on that wall. Each stack is six feet high and at its widest is six feet wide, occupying a square without filling it. In the first stack the left edge is flush and the right edge is irregular. In the second stack this relation is reversed, so in this one respect the first and second stacks are symmetrical while the lengths of the panels in the two stacks are not. It was a stroke of luck that the wall of the gallery was wide enough to comfortably contain two additional pairs of stacks, symmetrical in the same way as this first pair, giving a total of six stacks.

The negative spaces between the six stacks on the left-hand wall make the shapes of the six stacks on the right-hand wall. Where there is a panel six feet wide in a stack on the left-hand wall there is necessarily a void in the corresponding stack on the right-hand wall. Two corresponding stacks fill a square, so they are complements of each other. As this is true of corresponding stacks taken in pairs, it is true of all of the stacks on both walls taken together. The complementary relations in the painting are of two kinds: between the shapes of the stacks on either wall and the spaces between them and between the shapes of the corresponding stacks on the two walls.

6 × 6 × 6 × 2 asks the viewer to visualize the stacks on the right-hand wall fitting with the stacks on the left-hand wall or vice versa. The result of this act of imaginary translation would be a rectangular painting made of many contiguous panels. Like the two arrays on either wall, this imaginary painting would be six feet high and thirty-six feet long.

The colors in 6 × 6 × 6 × 2 come from the third edition of The Theory and Practice of Color by Bonnie E. Snow and Hugo B. Froehlich, published by The Prang Company, New York, in 1920. This book in its several editions is one of my favorite books.

Some further remarks.

I emphasize what is already clear, that within what I will call the schema of the work its specific appearance is a matter of chance. The panel I started with could have been two feet long and green or two feet long and yellow or three feet long and yellow or three feet long and green and so on instead of five feet long and violet. The panel above it could have been six feet long and red instead of two feet long and orange, and so on. The work as realized is the only one I worked out, but the chance procedure that made the work could have produced other instances. I asked a friend of mine with a Ph.D. in mathematics how many instances there could be. He said 3,110,400.

Because the work is the result of a chance procedure, each of these other possible instances is equally the work. The work as realized is what repeated rolls of a die happened to make that one time. I didn’t do several complete instances and pick the one I liked best. Because all possible instances are the result of chance, they are all the same work, and as such they are all equal. In my relation to them there is no occasion for my taste.

I had earlier thought it would be fun to make a book showing all the possible instances of the work. Each would be shown in a two-page spread. The pages would be wide in relation to their height. I knew it would be a thick book, but I didn’t realize how thick. The part of the book with the images would have 1,555,200 leaves. Supposing the paper were 100-pound coated paper, a sheet of which is 0.005 inches thick, the book would be 648 feet thick, plus a few pages at the beginning for a title page, etc., and a few at the end plus the covers. If the work were divided into volumes each six inches thick (plus the covers), there would be 1,296.

An issue in the book would be the order of the instances. A systematic order could persuade the viewer who looks at several successive instances that the book does probably include all possible permutations. But which systematic order? If it were to start as I did with the bottom panel of the left-hand stack on the left-hand wall, there would be many ways of proceeding systematically from there, as there would be starting from anywhere else, and I don’t know how to calculate them. A random order would avoid dealing with that question. The viewer would have to take it on faith that the book included each of the 3,110,400 instances.

If there isn’t a book, there could be an online version. Let’s duck the question of order and say that every visitor is shown a random instance. A counter could show the running total of all views. The visitor could do searches, so for each instance there could be two counters, one showing the number of views that are random, the other showing the number of views that are the result of a search. Instances I would search for are those in which the panels in the six stacks decrease in width from bottom to top or from top to bottom. In either instance the colors would be in order—red, orange, yellow, green, blue, violet—from bottom to top or top to bottom. These four instances wouldn’t look random, but they’re just as possible as each of the 3,110,396 others.